前言
如你所见,这是一篇连初中蒟蒻都能食用的预习文章,高中的dalao也可以用来复习。
高中花两三个礼拜才学完,现在只需一两个小时,还不来学
话不多说,直接凯驰。
集合的概念
知识点:
集合,小学三年级都学过,就是把一些同类的东西——如数字、学科、爱好之类的——放在一起,简称集。然后里面的东西叫做元素。
举个例子,由偶数组成的集合叫做偶数集,里面的元素有$0,2,4,6,8......$
只要构成两个集合的元素是一样的,我们就说这两个集合相等。
比如设$A$是偶数集,$B$是2的的倍数集,那么集合$A$和$B$相等,记做$A=B$。
这里有几个常用的集合可以背一下:
| 非负整数集 | 正整数集 | 整数集 | 有理数集 | 实数集 |
|---|---|---|---|---|
| $N$ | $N^*$或$N_+$ | $Z$ | $Q$ | $R$ |
如果$a$是集合$A$的元素,我们就说a属于A,记做$a \in A$ ; 否则就说a不属于A,记做$a \notin A$。
比如说设$A$为偶数集,则$2 \in A$,$1 \notin A$。
把一个集合的所有元素列举出来表示集合的方法叫做列举法;用集合内所有元素的共同特征表示集合的方法叫做描述法。
什么意思呢?
举个例子,设集合$A$表示$10$以内的奇数,那么用列举法就是$A=${$1,3,5,7,9$},用描述法就是$A={2x+1|x \in Z,且0 \le x \le 4}$。
例题:
用不同方法表示$20$的约数集,并判断$1,3,7,10$是否属于该集合。
解:
列举法:$A={$1,2,4,5,10,20}$;
描述法:$A={x|x \in N+,且xy=20,y \in N+}$;
$1 \in A,3 \notin A,7 \notin A,10 \in A$.
集合的基本关系
知识点:
小学学过集合的都看过这个图吧,它叫做Venn图,用来表示集合间的关系的。
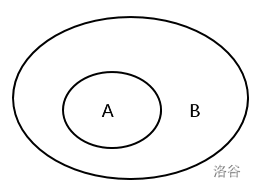
如果两个集合间的关系像上面那个图,也就是集合$A$的每一个元素都是集合$B$的元素,我们就说$A$包含于$B$,记做$A \subseteq B$,其中集合$A$是集合$B$的子集。
特别的,如果$A \subseteq B$,且$A \ne B$,那么我们说$A$真包含于$B$,记做$A \subsetneqq B$,其中集合$A$是集合$B$的真子集。
举个例子,设$A$是等腰三角形集合,$B$是等边三角形集合,$C$是正三角形集合,则$A \subsetneqq B$,$A \subsetneqq C$,$B \subseteq C$,$C \subseteq B$。
小知识:一个集合的子集一定有它本身。
子集的迭代性:若$A \subseteq B$,且$B \subseteq C$,则$A \subseteq C$。
什么元素都没有的集合叫做空集,记做$\varnothing$。
性质:空集是任意集合的子集。
例题:
判断以下哪些集合是$A=${$4x|x \in Z$}的子集。
$B=${$2x|x \in Z$},$C=${$16x|x \in Z$},$D=${$4,8,12,16,20$},$E=${$8^x|x \in N^*$},$\varnothing$.
解:
$C \subseteq A$,$E \subseteq A$,$\varnothing \subseteq A$.
集合的基本运算
知识点:
对,你没听错,集合之间还有运算。
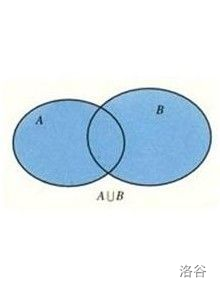
设有两个集合$A,B$,我们把组成这两个集合的所有元素组成的集合叫做集合$A$与$B$的并集,记做$A \cup B$,读作$A$并$B$,即$A \cup B=${$x|x \in A,或x \in B$}。
看上面那个Venn图,两个圆表示集合$A$和$B$,蓝色部分就是$A$并$B$。

设有两个集合$A,B$,我们把同是两个集合中的元素组成的集合叫做集合$A$与$B$的交集,记做$A \cap B$,读作$A$交$B$,即$A \cap B=${$x|x \in A,且x \in B$}。
看上面那个Venn图,两个圆表示集合$A$和$B$,粉色部分就是$A$交$B$。
小知识:$A \cup A=A \cup \varnothing=A \cap A=A$,$A \cap \varnothing=\varnothing$。

一个问题中所有元素组成的集合叫做全集,通常用字母$U$表示。
在全集$U$中,对于集合$A$,属于全集$U$但不属于集合$A$的元素组成的集合叫做在全集$U$中对于集合$A$的补集,记做$\complement_UA$,即$\complement_UA=${$x|x \in U,且x \notin A$}。
看上面那个Venn图,圆表示集合$A$,斜线部分就是$\complement_UA$,整个矩形表示全集$U$。
例题:
设全集$U=Z$,集合$A=${$2x|x \in N$},$B=${$x|0 \le x \le 10,且x \in N$},求$A \cap B$与$\complement_UB$。
解:
$A \cap B=${$2x|0 \le x \le 5,且x \in N$};
$\complement_UB=${$x|x>5或x<0,且x \in Z$}。
充分条件与必要条件
知识点:
如果由条件$p$能得到结论$q$,我们就称$p$推出$q$,记做$p \Rightarrow q$,其中$p$是$q$的充分条件,$q$是$p$的必要条件。
比如说,"等边三角形的每个角都是$60^\circ$"中,"等边三角形"是充分条件,"每个角都是$60^\circ$"是必要条件。
如果$p \Rightarrow q$,且$q \Rightarrow p$,我们就称$p$和$q$可以互相推出,记做$p \Leftrightarrow q$,其中$p$和$q$互为充分必要条件,简称充要条件。
举个例子,勾股定理与勾股定理的逆定理中,"直角三角形"与"直角边的平方和等于斜边的平方"互为充要条件。
例题:
指出下列命题的充分条件与必要条件。
(1)两直线平行,内错角相等;
(2)两点确定一条直线;
(3)若一个四边形的一组对边平行且相等,则该四边形为平行四边形。
解:
(1)充分条件:两直线平行;必要条件:内错角相等;
(2)充分条件:在同一平面内有两点;必要条件:有且只有一条直线过这两点;
(3)充分条件:一个四边形的一组对边平行且相等;必要条件:该四边形为平行四边形。
全称量词与存在量词
知识点:
在命题中,"所有的""任意一个"之类的词语称为全称量词,用符号$\forall$表示,该命题称为全称量词命题。
比如说,"所有的$4$的倍数都是偶数"是全称量词命题。
在命题中,"存在一个""至少有一个"之类的词语称为存在量词,用符号$\exists $表示,该命题称为存在量词命题。
比如说,"素数中至少有一个偶数"是存在量词命题。
命题中,通常用符号$\neg$表示否定。
全称量词命题$\forall x \in M,p(x)$的否定:$\exists x \in M,\neg p(x)$;
存在量词命题$\exists x \in M,p(x)$的否定:$\forall x \in M,\neg p(x)$。
例题:
判断下列命题是全称量词命题还是存在量词命题,并写出该命题的否定。
(1)$\forall x \in R,x \in Q$;
(2)$\exists x \in${$x|x17$。
解:
(1)全称量词命题,否定:$\exists x \in R,x \notin Q$;
(2)存在量词命题,否定:$\forall x \in${$x|x<0,且x \in Z$}$,x \le 17$。
后记
好了,这些知识点就用例题与知识点结合的方式水讲完了,没学会的多看例题理解亿下。
接下来是作业,记得写,下节课开头有答案。
作业:
1.
写出以下集合。
(1)偶数集;
(2)不等式$\frac{x+1}{5}+\frac{x-2}{2}0$。

Comments NOTHING